Chemie-Arbeitsblatt _ _ Klasse _ _ _ Name __________________________________________________________________Datum _ _ ._ _._ _
 

Kristallstrukturen (I)
 
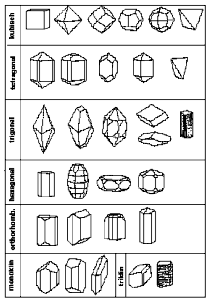Kristalle lassen sich aufgrund der Symmetrien ihrer Elementarzellen in 7 verschiedene Kristallsysteme einordnen:
  • Kubisch (oft regulär genannt)
  • Hexagonal
  • Trigonal (oft rhomboedrisch genannt)
  • Tetragonal
  • Rhombisch
  • Monoklin
  • Triklin

Manchmal wird das trigonale mit dem hexagonalen System zusammengefasst.
Die Grundstruktur, die aus den Abbildungen so einfach nicht ersichtlich ist, ist das Prisma, definiert als Körper, bei dem 2 gegenüberliegende Flächen gleich groß und parallel zu einander liegen. Das Prisma ist der Körper des Systems mit der maximalen Symmetrie.

Die Symmetrie der Elementarzellen
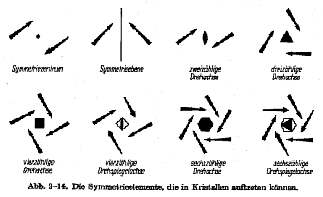
Die Symmetrie eines Körpers erhält man, indem man Ebenen sucht, die den Körper in zwei spiegelbildlich gleiche Hälften aufteilt. Diese Flächen nennen wir Symmetrie-Ebenen. Beim Suchen nach Symmetrie-Ebenen darf die Elementarzelle nicht gedreht werden, sondern muß immer von einer Seite, Kante oder Ecke her betrachtet werden.
Eine andere Symmetrie-Operation ist die Ermittlung der Zähligkeit von Drehspiegelachsen. Durch Drehung um diese Achse kann man feststellen, wie oft im Laufe einer Drehung um 360 ° gleiche Flächen bzw. Flächenkombinationen auftreten: Wenn dies nach einer Drehung von 180 ° der Fall ist, spricht man von einer zweizähligen Achse (rhombisch, monoklin), bei einer Drehung um 120 ° von einer dreizähligen (trigonal), um 90 ° von einer vierzähligen (kubisch, tetragonal) und schließlich bei einer Drehung um 60 ° von einer sechszähligen Achse (hexagonal). Z. B. hat der kubische Würfel drei vierzählige Drehspiegelachsen, die dazu noch rechtwinklig aufeinander stehen.
   
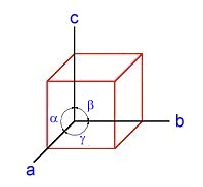
Beim kubischen Kristallsystem sind alle Achsen gleichlang, und die Winkel betragen 90 ° : a = b = c und
" = $ = ( = 90 ° .

Zum kubischen Kristallsystem zählen alle Kristallformen, die sich auf ein rechtwinkliges Achsenkreuz von drei gleich langen Achsen beziehen lassen.

Dazu gehören Bleiglanz, Diamant, Flußspat, Pyrit, Steinsalz, Zinkblende, Granat, Magnetit, Gold und Silber.
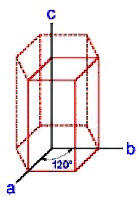
Zum hexagonalen Kristallsystem werden alle Kristallformen gerechnet, die sich auf ein schiefwinkliges Achsenkreuz von vier Achsen beziehen, von denen drei gleich lang sind und sich unter einem Winkel von 60 ° bzw. 120 ° schneiden. Die vierte Achse steht senkrecht zu den anderen: a = b … c und " = $ = 90 ° und
( = 120 °.

Zum hexagonalen Kristallsystem zählen Beryll, (Hoch-)Quarz, die Quarzmodifikation $-Tridymit, Wassereis und Graphit.
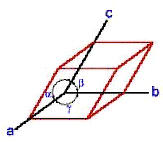
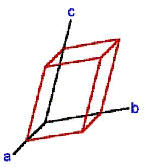
Das trigonale (oft: rhomboedrische) Kristallsystem ist ähnlich wie das hexagonale, es liegt ein schiefwinkliges Achsenkreuz vor. Drei Achsen sind gleich lang, schneiden sich allerdings in unterschiedlichen Winkeln.

Es gilt: a = b = c und " = $ = ( … 90 °.

Zum trigonalen Kristallsystem zählen (Tief-)Quarz, Calcit und Chrom.
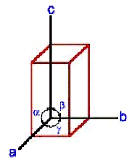
Auch bei dem tetragonalen Kristallsystem liegt ein rechtwinkliges Koordinatensystem vor. Zwei Koordinatenachsen sind gleich lang, senkrecht dazu steht eine längere (oder kürzere) Achse.

Also: a = b … c und " = $ = ( = 90 °

Zum tetragonalen System zählen Rutil und Zirkon.
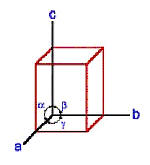
Zum rhombischen Kristallsystem werden alle Kristallformen gezählt, die sich auf ein rechtwinkliges Achsenkreuz beziehen, dessen drei Achsen verschieden lang sind.

Also gilt: a … b … c und " = $ = ( = 90 °

Zum rhombischen Kristallsystem zählen Baryt, Schwefel, Markasit, Aragonit, Cölestin und Spateisenerz.
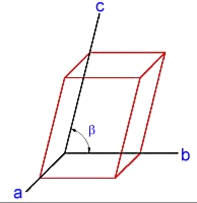
Die Kristallformen des monoklinen Kristallsystems lassen sich auf ein schiefwinkliges Achsenkreuz beziehen, dessen drei Achsen unterschiedlich lang sind. Zwei Achsen schneiden sich in einem rechten Winkel.

Es gelten also folgende Regeln: a … b … c und " = ( = 90 ° und $ … 90 °

Zum monoklinen Kristallsystem zählen Rohrzucker, rotes Blutlaugensalz, Gips, Kalifeldspat, Malachit und Asbest.
Das trikline Kristallsystem umfasst alle Kristallformen, die sich auf ein schiefwinkliges Achsenkreuz beziehen, dessen drei Achsen ungleich lang sind und sich unter schiefen Winkeln schneiden.
Hier ist also: a … b … c und " … $ … ( … 90 °

Zum triklinen Kristallsystem zählen Kupfersulfat-Pentahydrat und Labradorit.
Die Kristallklassen

Wegen der Symmetrien der Prismen sollte es jedem leicht fallen, Kristalle ihrem System zuzuordnen. Wie alles in der Wissenschaft ist es natürlich viel, viel komplizierter. Die Kristallsysteme unterteilt man nämlich weiter in 32 Formengruppen ("Kristallklassen"). Das können wir am Beispiel des kubischen Systems erklären: Dessen Prisma ist rechtwinklig, die Kantenlängen sind alle identisch: Es ist der Würfel. Solche Kristalle kennst du vom Kochsalz, Flußspat oder Pyrit. Zum kubischen System gehören aber auch Doppelpyramiden (Oktaeder), Pentagondodekaeder, Rhombendodekaeder, Tetraeder, Ikosaeder und viele, viele mehr. Beispielsweise tritt der Diamant in den Formen Tetraeder, Oktaeder, Würfel und abgestumpfter Würfel auf. Das sind aber nicht etwa Modifikationen des Diamants, denn die Grundform ist und bleibt das kubische System mit seiner rechtwinkligen, gleichseitigen Elementarzelle. Nur äußere Bedingungen haben den Kristall veranlasst, aus der hochsymmetrischen, würfelförmigen kubischen Elementarzelle diese oder jene Wachstumsrichtung einzuschlagen. Gemeinsam ist diesen kubischen Körpern, dass sie sich auf die Würfel-Symmetrie zurückführen lassen, obwohl sie weniger Symmetrie-Ebenen aufweisen als das Grundprisma Würfel. Sie lassen sich aber alle in einen Würfel einzeichnen und haben dann wieder die Symmetrie des Grundprismas.

Arbeitsaufträge:

  1. Fasse die wesentlichen geometrischen Eigenschaften der 7 Systeme tabellarisch zusammen.
  2. Was unterscheidet Kristallsysteme von Kristallklassen?
  3. Erkläre das Auftreten verschiedener Klassen in den einzelnen Systemen!

Quelle:  leicht verändert nach  http://www.chemieunterricht.de/dc2/kristalle/index.html

 

update: 02.02.2021                                                                                                                                                                               zurück        zur Hauptseite