|
|||
Kristallstrukturen (II): Das kubische Kristallsystem |
|||
 Abb. 7: |
Das kubische
Kristallsystem ist besonders einfach. Es ist gekennzeichnet durch
einen hohen Grad an Symmetrie, erkennbar an den vier vierzähligen
Drehspiegelachsen. Was bedeutet das?
Legen wir in den Würfel ein rechtwinkliges Koordinatensystem, kommt man
durch Drehung um 360 °: 4 = 90 ° in die gleiche Position wie die
Ausgangslage. Dies gilt für jede der drei Raumrichtungen x, y und z. Es
gibt also erst einmal drei vierzählige Achsen. Alle kubischen Körper lassen sich in einen Würfel einzeichnen, z.B. der Tetraeder (siehe Abbildungen linke Seite). Zur Darstellung benutzt man die Diagonalen des Würfels (Tetraeder), die Flächenhalbierenden (Pentagondodekaeder) oder die Seitenmittelpunkte (Oktaeder oder Rhombendodekaeder). Umgekehrt lassen sich aber auch Würfel z.B. in einen Oktaeder einzeichnen. Auch ein Oktaeder lässt sich in einen Tetraeder einzeichnen. Und sogar ein Pentagon-dodekaeder geht in einen Oktaeder hinein. Stumpft man die 8 Ecken des Würfels so ab, dass wieder quadratische Flächen entstehen, erhält man den Kubooktaeder. Der Rhombendodekaeder besteht aus 12 Rauten, die nicht rechtwinklig sind, aber gleichseitig. Weitet man das Pentagondodekaeder durch weitere Sechsecke auf, bekommt man einen abgestumpften Eikosaeder, der oberflächlich einem Fußball oder chemisch den Fullerenen gleicht. Arbeitsaufträge:
|
 Abb. 1: Würfel |
|
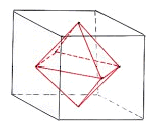 Abb. 8: |
 Abb. 2: Tetraeder |
||
 Abb. 9: |
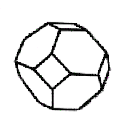 Abb. 3: Kubooktaeder |
||
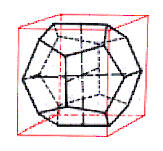 Abb. 10: |
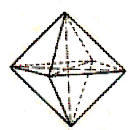 Abb. 4: Oktaeder |
||
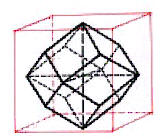 Abb. 11: |
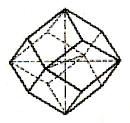 Abb. 5: Rhombendodekaeder |
||
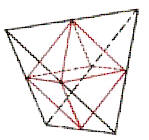 Abb. 12: |
Quelle:
http://www.chemieunterricht.de/dc2/kristalle/index.html
|
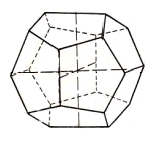 Abb. 6: Pentagondodekaeder |
|
|
|
|||