Kinetik der alkalischen Esterhydrolyse1. Voraussetzungen |
||||||||
|
Ein Ester reagiert mit Wasser in folgender Gleichgewichtsreaktion: Ester + Wasser <=========>Säure + Alkohol Die
Esterverbindung ist elektrisch nicht leitend.
Wird dem Ester Natronlauge zugesetzt, verläuft folgende
alkalische Hydrolyse-Reaktion
(alkalische Verseifung): |
||||||||
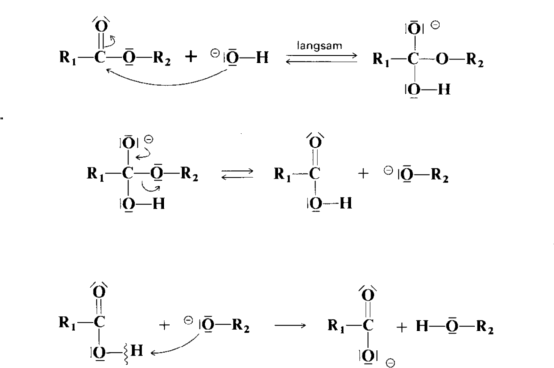 |
||||||||
| Die
Reaktion verläuft in
drei Schritten:
1.Nucleophiler Angriff des Hydroxid-Ions unter Bildung eines Additionsprodukts 2. Abspaltung des Alkoholat-Ions und Bildung der Carbonsäure 3. Protonenübergang vom Carbonsäure-Molekül auf das Alkoholat-Ion |
||||||||
| 2. Einsatz der Konduktometrischen Methode | ||||||||
| 3. Theorie des Messverfahrens | ||||||||
| Zum Ladungstransport tragen
bei der Reaktion die Natrium-Ionen Na+, die
Hydroxid-Ionen OH
– und die Acetationen Ac – bei. Deren
molare Ionenleitfähigkeit bei unendlicher Verdünnung besitzen bei 25 °C
die Werte: OH–: 199,2 S * cm2/mol, Ac –:
40,9 S * cm2/mol und Na+: 50,1 S * cm2/mol
Welche Beziehung besteht nun zwischen der Abnahme der Stromstärke und der Änderung der OH–-Konzentration? Nach einem Drei-Phasen-Modell können folgende
Abschnitte der Reaktion unterschieden werden: |
||||||||
|
a). Beginn der Reaktion
Zu Beginn der Reaktion (t = 0) liegen nur die Na+ - und OH–-Ionen vor. Die Stromstärke hat daher gemäß der allgemeinen Beziehung [4] I = a * ∑ (m(x) * c(x)) den Wert: I0 = ∑ I (x) = I(Na+) + I(OH–) [5] Die Stromstärke ist dabei proportional der Ladung und der Schnelligkeit, mit der die Ladung transportiert wird. Die Größe der Ladung und die Geschwindigkeit des Transports werden ausgedrückt im Faktor m(x) . Die Anzahl der Ladungsträger, also die Konzentration, spielt ebenfalls eine Rolle. Daraus ergibt sich die Beziehung: I0 ≈ c(x) * m(x) [6] Mit Einführung einer Proportionalitätskonstanten a(x) ergibt sich dann für das Na+-Ion der Stromstärken-Anteil: I(Na+) = a * m(Na+) * c(Na+) [7] Zu Beginn der Reaktion gilt dann für beide Ionen: I0 = (a * m(Na+) * c0(Na+)) + (a * m(OH–) * c0(OH–)) [8] Bezeichnet man die OH–-Konzentration zum Zeitpunkt t = 0 mit c0, so gilt aus Gründen der Elektroneutralität: c0(OH–) = c0(Na+) = c0 [9] Daraus folgt für die Stromstärke zum Zeitpunkt t = 0: [9] in [8]: I0 = (a * m(Na+) * c0) + (a * m(OH–) * c0)) [10] bzw. zusammengefasst: |
||||||||
|
||||||||
|
b) Reaktionsphase
I = (a * m(Na+) * c(Na+)) + (a * m(OH–) * c(OH–)) +(a * m(Ac–) * c(Ac–)) [13] Die Na+-Ionenkonzentration bleibt während der ganzen Reaktion konstant: c(Na+) = c0(Na+) = c0 [14] Im Gegensatz dazu ändert sich die OH–-Ionenkonzentration, da das Hydroxid-Ion in die Reaktion eingeht. Daher soll c(OH–) = c sein. [15] Aufgrund der Elektroneutralität gilt: c(OH–) + c(Ac–) = c(Na+) [16] Die Summe der negativen Ladungen muss gleich sein der Summe der positiven Ladungen: [14] und 15] in [16]: c + c(Ac–) = c0 [17] Daraus ergibt sich für die Ac–-Konzentration der Term: c(Ac–) = c0 - c [18] Wenn in Term [13] I = (a * m(Na+) * c(Na+)) + (a * m(OH–) * c(OH–)) + (a * m(Ac–) * c(Ac–)) [13] mit c(Na+) = c0 [14], c(Ac–) = c0 - c [18] und c(OH–) = c [15] folgende Substitutionen durchgeführt werden, ergibt sich der Ausdruck für die Stromstärke zum Zeitpunkt t: I = (a * m(Na+) * c0) + (a * m(OH–) * c) + (a * m(Ac–) * (c0 - c)) [19] bzw. I = (a * m(Na+) * c0) + (a * m(OH–) * c) + (a * m(Ac–) * c0) - (a * m(Ac–) * c) [20] Zusammengefasst:
|
||||||||
|
c) Endphase:
die Reaktion ist beendet. Am Ende der Reaktion bei t = ∞
liegen nur noch die Ac–- und die Na+-Ionen
in gleicher Konzentration c0 vor, da die OH–-Ionen ja verbraucht wurden: I∞ = I(Na+) + I(Ac–) [22] = (a * m(Na+) * c(Na+)) + (a * m(Ac–) * c(Ac–)) [23] Mit c(Na+) = c0 [14] und c(Ac–) = c0 - c [18] ergibt sich daraus: I∞ = (a * m(Na+) * c0) + (a * m(Ac–) * (c0 - c)) [24] und da c = c(OH–) [15] am Ende der Reaktion den Wert 0 erreicht hat, gilt: I∞ = (a * m(Na+) * c0) + (a * m(Ac–) * c0) [25] Somit gilt für die Stromstärke zur Zeit t = ∞ |
||||||||
|
||||||||
| Graphische Darstellung der verschiedenen Größen: | ||||||||
 |
||||||||
| Um aus den gemessenen
Stromstärken I0, I und I∞ die
gesuchte
Konzentration c zu erhalten, müssen die übrigen Unbekannten (a, m(Na+),
m(Ac–) und m(OH–) entweder experimentell bestimmt
oder durch passende mathematische
Operationen eliminiert werden.
m(Na+) lässt sich sehr einfach eliminieren, wenn man Stromstärkedifferenzen bildet: I0 - I∞ = (a * c0 * (m(Na+) + m(OH–))) - (a * c0 * (m(Na+) + m(Ac–))) [27] = (a * c0 * m(Na+)) + (a * c0 * (m(OH–)) - (a * c0 * m(Na+)) - (a * c0 * (m(Ac–)) [28]
Für die zweite Differenz gilt:
= (a * c0
* (m(Na+)) + (a * c0 * m(Ac–)) + (a * c
* (m(OH–)) - (a * c * m(Ac–)) - (a * c0
* = (a * c * m(OH–)) - (a * c * m(Ac–)) [32]
Zwischenergebnis:
|
||||||||
|
(I0
- I∞)
= a * c0 *
(m(OH–) - a * c0
* m(Ac–) (I - I∞) a * c * (m(OH–) - a * c * m(Ac–) [34]
= a *
(m(OH–) - a * m(Ac–)
* c0 (I0
- I∞)
= c0 Dann ist
Da die Stromstärke der Leitfähigkeit proportional ist, gilt diese Gleichung auch für die Leitfähigkeit:
|
||||||||
|
4.
Anwendung:
siehe Arbeitsblatt „Reaktionen 2. Ordnung" 5. Auswertung: siehe Text „Auswertung des Versuchs zur alkalischen Esterhydrolyse" |
||||||||
Literatur: Tausch/v. Wachtendock: Chemie SII; Stoff - Formel - Umwelt; C.C. Buchner-Verlag. Bamberg 1993 Lutz Strohmaier: Chemie Sekundarstufe II, Verlauf chemischer Reaktionen; Schwann Verlag Düsseldorf 1978 |
||||||||
|
|