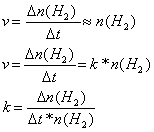Wie erstellt man eine Geschwindigkeitskonstante? |
|||||||||||||||||||||||||||||||||||||||||||||
|
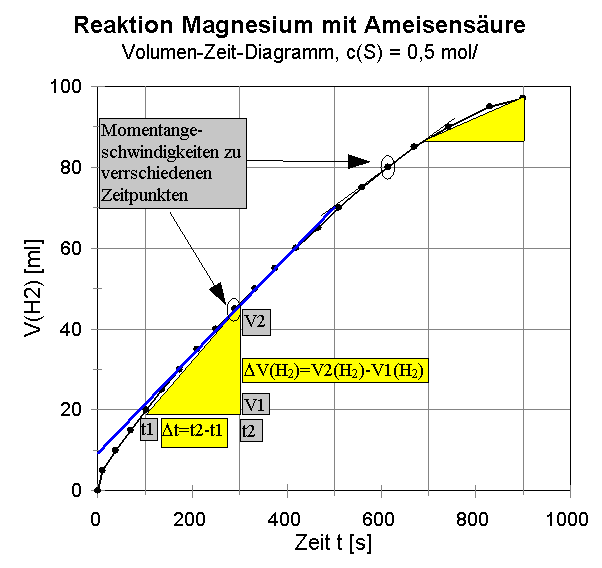
1. Schritt: Durchführung eines Versuchs wie V5 im AB “Versuche zur Reaktionsgeschwindigkeit”. 2. Schritt: Erstellung eines Volumen-Zeit-Diagramms: Dabei wird auf der x-Achse die Zeit t in [s] und auf der y-Achse das Volumen Wasserstoff V(H2) [mL] eingetragen und die Punkte mit einem Kurvenlineal oder von Hand graphisch interpolierend verbunden. Ob man im Experiment von vorgegebenen Zeitabschnitten (z.B. 10 s-Takt) oder von vorgegebenen Volumenabschnitten ausgeht, spielt keine Rolle: inhaltlich ist in jedem Fall die Zeit die unabhängige Variable und das Volumen die abhängige Variable. Das Diagramm (Abb. 1) zeigt die Abnahme entsprechender Durchschnittsgeschwindigkeiten in verschiedenen Zeitabschnitten. Die
Durchschnittsgeschwindigkeit ist die Steigung der Sekante im
Zeitabschnitt t2-t1, wobei t2 immer 3. Schritt: Lässt man die Zeitabschnitte gegen Null wandern, bestimmt
also die Grenzwerte der Differenze 4. Schritt: Um den Versuch mit ähnlichen Versuchen vergleichbar zu machen, wird vom konkreten Volumen Wasserstoff V(H2) auf die Molzahl n(H2) umgerechnet: n(H2) = V(H2) /Vmn = V(H2) [mL] / 24000 [mL/mol] bei 25 °C und 1013 hPa. Das molare Normvolumen Vmn eines Gases ist eine Naturkonstante und beträgt 22,414 L/mol bei 0 ̊ C und 1013 hPa. 5. Schritt: Das nun erstellte Diagramm n(H2)/t unterscheidet sich nicht wesentlich vom V(H2)/t-Diagramm, es beantwortet nur allgemeiner z.B. die Frage, wie viel Mol Wasserstoffgas sich in welcher Zeit entwickeln. Ob die Reaktionsgeschwindigkeit jedoch alleine von der Säurekonzentration oder der Masse Magnesium oder von beiden Faktoren abhängt, kann es ebensowenig beantworten. Also werden wir dieses Diagramm nicht weiter betrachten! Deswegen wird nun im 6. Schritt ein Diagramm erstellt bzw. berechnet, das diese Frage beantworten soll. Das Verfahren geht folgendermaßen vor sich (siehe Aufbau der Tabelle 1): aus den Zeitwerten t1, t2, t3, t4 usw. werden Differenzen erstellt: Δt= t2-t1, usw. Aus den Molzahlen werden ebenfalls entsprechende Differenzen erstellt: Δn(H2) = n2(H2) - n1(H2) usw. Generell wird der kleinere Wert vom größeren abgezogen, das Ergebnis ist eine positive Zahl. Im 7. Schritt werden nun die berechneten Werte graphisch aufgetragen: die Molzahlen, also n(H2), werden auf der x-Achse abgetragen, der Quotient Δn(H2)/Δt, der ja die Veränderung der Molzahlen pro Zeiteinheit darstellt, also die Reaktionsgeschwindigkeit, auf der y-Achse. Das erste Differenzenpaar bezieht sich auf den ersten realen Wert von n(H2), das zweite Paar auf den 2. Wert usw. Wird das erste Differenzenpaar weggelassen, weil es die Werte Null/Null einbezieht, also den Ursprungsort des Graphen, ist auch der entsprechende Wert von n(H2) wegzulassen. Im Diagramm erhält
man nun eine Reihe von Punkten, die mehr oder weniger auf einer Geraden liegen.
Diese Gerade zeichnet man als Linie per Tabellenkalkulationsprogramm oder von
Hand ein: es ist eine sog.
Regressionsgerade. Der 1. Wert weicht meistens grob davon ab, weil er
entweder den Ursprungsort (0/0) einbezieht bzw. die fast immer größere
Anfangsgeschwindigkeit mit einbezieht. Er wird deswegen vernachlässigt. Die
Steigung der Geraden ist der Wert der
Geschwindigkeitskonstante k: Die Reaktionsgeschwindigkeit sinkt mit
steigender Molzahl H2-Gas, also mit abnehmender Säurekonzentration,
weil die Zunahme des Gasvolumens direkt proportional der Abnahme der H+-Ionen
der Säure ist (siehe Reaktionsgleichung). Das Verfahren heißt
numerische Differentation.
Die Formelbox zeigt die mathematischen Zusammenhänge. Der Vergleich
verschiedener k-Werte bei unterschiedlichen Reaktionsbedingungen beantwortet die
obige Fragestellung, wie die Konzentration eines Edukts oder eines zweiten oder
beider Edukte die Reaktionsgeschwindigkeit beeinflusst.
Abb.1.:
Volumen-Zeit-Diagramm mit Angabe zweier verschiedener Durchschnittsgeschwindigkeiten zu zwei
Tabelle 1:
Tab.1.: Umwandlung der V(H2)-Werte in n(H2) und die Bildung entsprechender Differenzen bzw. Differenzenquotienten
10
Abb.
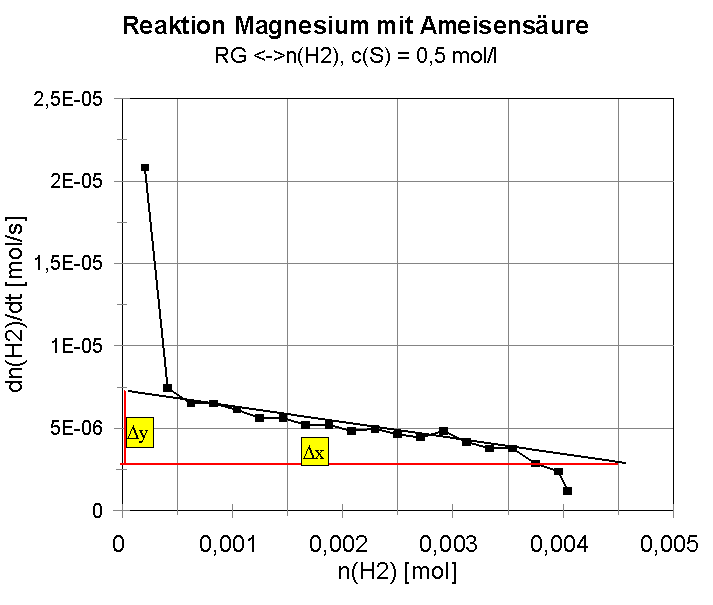
2: Die im letzten Schritt aufgetragenen Wertepaare n(H2)
gegen Δn(H2)/Dt
ergeben einen Punktereihe.
|
|||||||||||||||||||||||||||||||||||||||||||||
| update: 30.01.2021 zurück zur Hauptseite |
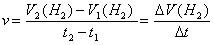
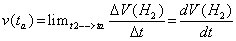 nquotienten,
werden aus den Differenzenquotienten
nquotienten,
werden aus den Differenzenquotienten