|
Wasser wird durch elektrischen Strom in
Wasserstoff- und Sauerstoffgas zersetzt. Lässt man umgekehrt
Wasserstoff- und Sauerstoffgas in einer Brennstoffzelle miteinander
reagieren, kann man daraus direkt elektrischen Strom gewinnen. Auf diese
Weise bekommt z.B. ein Brennstoffzellenmotor seine Energie zum Betrieb
eines Fahrzeugs. Die Energie zum Zerlegen von Wasser kann z.B. aus
Sonnenenergie gewonnen werden über die sog. Photovoltaik (Umwandlung von
Lichtenergie in elektrischen Strom).
Welche quantitativen Zusammenhänge existieren nun zwischen der Menge des
geflossenen Stroms und den abgeschiedenen Stoffmengen? Zur Klärung
dieser Frage wird in einem Hoffmann'schen Wasserzersetzungsapparat mit
Schwefelsäure versetztes Wasser [c(H2SO4) = 0,5 mol/l] für eine
definierte Zeit mit einer ganz bestimmten Gleichspannung und Stromstärke
elektrolytisch zerlegt. Die Messergebnisse werden in den folgenden
Tabellen notiert. Die Versuche werden gruppenarbeitsteilig durchgeführt.
Die vorgegebene Spannung wird am Gerät eingestellt, die Stromstärke
während des Betriebs gemessen.
Versuchsdurchführung:
1. Notiere zuerst Luftdruck:
______ hPa, und Raumtemperatur:
____ ̊C
2. Kontrolliere die Funktionsfähigkeit der Versuchsanordnung
(Füllstand in beiden Schenkeln des Wasserzersetzungsapparats,
eingestellte Spannung, Kabelverbindungen u.a.) |
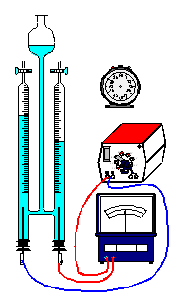 |
| 3. Beobachte ständig das Ausgleichsgefäß: wenn es
überzulaufen droht, entnimmt mit der Pipette entsprechend viel
Schwefelsäure! |
Arbeitsaufträge:
1. Notiere die Volumina Wasserstoff- und Sauerstoffgas in
Abhängigkeit von der Zeit!
2. Stelle für deinen Versuch die Messergebnisse auf
Millimeter-Papier graphisch dar!
3. In welchem Verhältnis stehen die Volumina Wasserstoff und
Sauerstoff bei allen Messungen?
3. Welcher quantitative Zusammenhang besteht zwischen dem
abgeschiedenen Gasvolumen, der Art des Gases, Stromstärke und der Zeit?
4. Berechne den Zusammenhang zwischen geflossener Ladung und der
Stoffmenge n(X) mit X=H2 bzw. O2 |
Zusatzinformation:
Messwerte-Tabelle: |
 |
 |
| t [min] |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
| V(H2) [ml] |
|
|
|
|
|
|
|
|
|
|
U = 8 V
I = _____ mA |
| V(O2) [ml] |
|
|
|
|
|
|
|
|
|
|
| V(H2) [ml] |
|
|
|
|
|
|
|
|
|
|
U =
10 V
I = _____ mA |
| V(O2) [ml] |
|
|
|
|
|
|
|
|
|
|
| V(H2) [ml] |
|
|
|
|
|
|
|
|
|
|
U = 12 V
I = _____ mA |
| V(O2) [ml] |
|
|
|
|
|
|
|
|
|
|
| V(H2) [ml] |
|
|
|
|
|
|
|
|
|
|
U =
14 V
I = _____ mA |
| V(O2) [ml] |
|
|
|
|
|
|
|
|
|
|
| V(H2) [ml] |
|
|
|
|
|
|
|
|
|
|
U = 20 V
I = _____ mA |
| V(O2) [ml] |
|
|
|
|
|
|
|
|
|
|
|
|
Lösungen: |
Arbeitsaufträge:
1. Notiere die Volumina Wasserstoff- und Sauerstoffgas in
Abhängigkeit von der Zeit!
| t [min] |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
| V(H2) [ml] |
2 |
3,2 |
4,4 |
5,6 |
6,8 |
8 |
9,2 |
10, |
11,6 |
12,8 |
U = 8 V
I = _____ mA |
| V(O2) [ml] |
1 |
2 |
2,8 |
3,2 |
3,8 |
4,4 |
5 |
5,6 |
6,2 |
6,8 |
| V(H2) [ml] |
4,2 |
4,8 |
6,8 |
8,6 |
10,6 |
12,6 |
14,4 |
16,3 |
18,2 |
20 |
U = 10 V
I = _____ mA |
| V(O2) [ml] |
3,3 |
3,4 |
4,2 |
5,2 |
6,2 |
7,2 |
8,2 |
9,1 |
10,1 |
11 |
| V(H2) [ml] |
3,8 |
6,4 |
9,0 |
11,4 |
13,8 |
16,4 |
19 |
21,4 |
24,2 |
26,2 |
U = 12 V
I = _____ mA |
| V(O2) [ml] |
3,4 |
3,6 |
5,0 |
6,6 |
7,4 |
8,6 |
9,8 |
11,0 |
12,8 |
13,8 |
| V(H2) [ml] |
3,8 |
7,8 |
12,0 |
15,4 |
18,0 |
21,8 |
25,0 |
29,8 |
33,2 |
36,6 |
U = 14 V
I = _____ mA |
| V(O2) [ml] |
2,0 |
4,0 |
6,2 |
8,0 |
9,4 |
11,2 |
13,0 |
15,6 |
17,4 |
19,0 |
| V(H2) [ml] |
5,8 |
10,5 |
15,2 |
18,6 |
24,3 |
29,4 |
35,1 |
42,7 |
--- |
--- |
U = 20 V
I = _____ mA |
| V(O2) [ml] |
3,8 |
6,1 |
8,3 |
10,6 |
13,0 |
15,2 |
17,8 |
21,4 |
--- |
--- |
|
2. Stelle für deinen Versuch die Messergebnisse auf
Millimeter-Papier graphisch dar!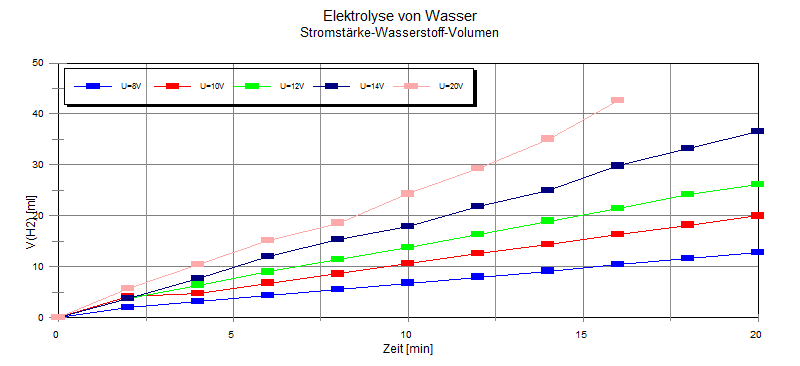

Neben dieser Darstellungsart gibt es noch andere Möglichkeiten. |
|
3. In welchem Verhältnis
stehen die Volumina Wasserstoff und
Sauerstoff bei allen Messungen? Bei allen
Messungen ist das Volumen Wasserstoff ungefähr doppelt so groß wie das
Sauerstoff-Volumen. Die Volumina von Wasserstoff und Sauerstoff stehen
also im Verhältnis 2 : 1 .
|
|
3. Welcher quantitative Zusammenhang
besteht zwischen dem
abgeschiedenen Gasvolumen, der Art des Gases, Stromstärke und der Zeit?
Unabhängig von der verwendeten Spannung ist das
abgeschiedene Gasvolumen der Zeit proportional:
t
≈
V(Gas)
Unabhängig von der Zeit ist das
abgeschiedene Gasvolumen der angelegten Spannung
proportional:
V(Gas) ≈ U
Unabhängig von der Zeit und der
angelegten Spannung ist das abgeschiedene
Gasvolumen von der Art des
Gases abhängig (s.o.)
Da ursächlich nicht die Spannung für die Abscheidung
verantwortlich ist, sondern die Stromstärke, die wiederum der Spannung
proportional ist, muss es heißen: Das abgeschiedene Gasvolumen ist der
Zeit und der Stromstärke proportional:
V(Gas) ≈ I * t
|
|
4. Berechne den Zusammenhang zwischen geflossener Ladung und der
Stoffmenge n(X) mit X=H2 bzw. O2
Bei einem Druck von 1013 hPa und einer Temperatur
von 25 °C ändert sich das Molare (Norm)Volumen Vmn
von 22414 mL auf 24467 mL.
Die Stoffmenge errechnet sich aus
der Gleichung n(Gas) = V(Gas)
/ Vmn(Gas) (1) und der Allgemeinen
Zustandsgleichung der Gase:
p * V / T = pn * Vmn
/ Tn
(2) mit pn = 1013 hPa und Tn = 273K = 0 °C. T
= 25 °C = 298 K.
|
Zusammenhang zwischen
abgeschiedener Stoffmenge und Ladung Q = I*t [A*s] bei U=10V |
|
|
t [min] |
n(H2) |
n(O2) |
I*t [As] |
I*t/n(H2 |
%Abw-MW |
I*t/n(O2) |
%Abw-MW |
k(H2)/k(O2) |
|
2 |
7,28E-05 |
3,88E-05 |
15,60 |
214.426 |
-2,32% |
401.767 |
-2,54% |
0,53 |
|
4 |
1,45E-04 |
7,77E-05 |
31,20 |
215.030 |
-2,05% |
401.767 |
-2,54% |
0,54 |
|
6 |
2,08E-04 |
1,10E-04 |
46,80 |
224.517 |
2,27% |
424.087 |
2,87% |
0,53 |
|
8 |
2,82E-04 |
1,51E-04 |
62,40 |
221.263 |
0,79% |
412.625 |
0,09% |
0,54 |
|
10 |
3,56E-04 |
1,88E-04 |
78,00 |
219.355 |
-0,08% |
414.868 |
0,64% |
0,53 |
|
12 |
4,25E-04 |
2,29E-04 |
93,60 |
220.199 |
0,31% |
408.941 |
-0,80% |
0,54 |
|
14 |
4,95E-04 |
2,62E-04 |
109,20 |
220.806 |
0,58% |
417.461 |
1,27% |
0,53 |
|
16 |
5,72E-04 |
3,07E-04 |
124,80 |
218.102 |
-0,65% |
407.124 |
-1,24% |
0,54 |
|
18 |
6,36E-04 |
3,35E-04 |
140,40 |
220.907 |
0,63% |
418.915 |
1,62% |
0,53 |
|
20 |
7,07E-04 |
3,76E-04 |
156,00 |
220.623 |
0,50% |
414.868 |
0,64% |
0,53 |
| |
MW |
219.523 |
-0,00 |
412.242 |
0,00% |
0,53 |
|
Zusammenhang zwischen abgeschiedener Stoffmenge
und Ladung Q = I*t [A*s] bei U=20V |
|
|
t [min] |
n(H2) |
n(O2) |
I*t |
I*t/n(H2) |
%Abw-MW |
I*t/n(O2) |
%Abw-MW |
k(H2)/k(O2) |
|
2 |
1,68E-04 |
8,58E-05 |
39,60 |
236.311 |
4,87% |
461369 |
4,82% |
0,51 |
|
4 |
3,60E-04 |
1,84E-04 |
79,20 |
220.199 |
-2,28% |
430612 |
-2,17% |
0,51 |
|
6 |
5,40E-04 |
2,74E-04 |
118,80 |
220.199 |
-2,28% |
433825 |
-1,44% |
0,51 |
|
8 |
6,99E-04 |
3,60E-04 |
158,40 |
226.638 |
0,57% |
440398 |
0,06% |
0,51 |
|
10 |
8,79E-04 |
4,50E-04 |
198,00 |
225.320 |
-0,01% |
440398 |
0,06% |
0,51 |
|
12 |
1,05E-03 |
5,40E-04 |
237,60 |
225.320 |
-0,01% |
440398 |
0,06% |
0,51 |
|
14 |
1,23E-03 |
6,29E-04 |
277,20 |
225.320 |
-0,01% |
440398 |
0,06% |
0,51 |
|
16 |
1,41E-03 |
7,28E-04 |
316,80 |
224.667 |
-0,30% |
435450 |
-1,07% |
0,52 |
|
18 |
1,59E-03 |
8,13E-04 |
356,40 |
224.162 |
-0,53% |
438185 |
-0,44% |
0,51 |
|
20 |
1,76E-03 |
8,99E-04 |
396,00 |
225.320 |
-0,01% |
440398 |
0,06% |
0,51 |
| |
MW |
225.346 |
-0,00 |
440.143 |
-0,00% |
0,51 |
Entsprechend der Reaktionsgleichung 2
H2O (l) ---> 2 H2(g) + O2(g) werden
zur Abscheidung von 2 H2(g) vier Elektronen benötigt, also
für 1 H2(g)-Molekül nur 2 Elektronen. Bei der Abscheidung von
1 O2(g) werden vier Elektronen freigesetzt. Die Anzahl der
abgeschiedenen Teilchen ist also abhängig von der Zahl der aufgenommenen
oder abgegebenen Elektronen: Je größer die Anzahl der
aufgenommenen/abgegebenen Elektronen für das betreffende Ion/Atom, desto
geringer die Teilchenzahl der abgeschiedenen Stoffe.
Die Anzahl der aufgenommenen oder
abgeschiedenen Elektronen ist proportional zur Ladung Q, die zur
Abscheidung einer bestimmten Stoffmenge benötigt wird:
Q
≈ z
mit z = Anzahl der aufgenommenen oder abgegebenen Elektronen. Für
beide abgeschiedenen Stoffe war Q im Versuch bei bestimmten Spannungen
und Zeitdauer gleich. Da mit z = Anzahl der aufgenommenen oder
abgegebenen Elektronen jeweils eine Einheit des Teilchen verbunden ist,
als X, muss es genauer heißen:
Q
≈ z * n(X).
Für die
Abscheidung von Wasserstoff (X=H2) ist z=2, für X=O2
ist z=4, also Q/2 für H2 und Q/4 für O2.
Setzt man für Q
einen beliebigen gleichen Wert ein, wird deutlich, dass dann für
Wasserstoff doppelt so viele Teilchen abgeschieden werden wir für
Sauerstoff. |
update: 10.02.2021
zurück
zur Hauptseite |