|
Aus kinetischen Untersuchungen von Reaktionsverläufen kann man
Rückschlüsse auf den Reaktionsmechanismus ziehen.
Zur Erinnerung:
Ein Reaktionsmechanismus
beschreibt die einzelnen Schritte des Bindungsbruchs und der
Bindungsneubildung, die sich zwischen den reagierenden Partnern
abspielen:
„Unter
dem Reaktionsmechanismus einer organisch-chemischen Reaktion versteht
man die Gesamtheit aller Einzelphasen und Teilreaktionsstufen, deren
Ablauf zeitlich sowohl neben- als auch nacheinander erfolgt."
(G. Graeb: Reaktionen und Mechanismen, DBV)
Erkenntnisse über diese einzelnen Schritte des
Bindungsbruchs und der -neubildung gewinnt die Chemie u.a. aus
Untersuchungen der Reaktionsgeschwindigkeit (RG):
Wie
ändert sich die Reaktionsgeschwindigkeit in Abhängigkeit von der
Konzentration der Ausgangs- oder Endstoffe?
Reagieren zwei Stoffe A und
B zu C und D,
muss die Stöchiometrie dieser Reaktion nicht identisch sein mit den
elementaren Vorgängen, die bei der Verbindungsneubildung ablaufen. Es
kann sein, dass aus dem Zusammenstoß von A und B die Folgeprodukte C und D
entstehen, es kann aber auch sein, dass unabhängig von Stoff B der Stoff
A irgendwelche Veränderungen durchmacht, die Voraussetzung der weiteren
Reaktion mit Stoff B sind. Bei der Untersuchung von Reaktionsgeschwindigkeiten ist
eine der zentralen Grundannahmen, dass der langsamste Schritt
einer in mehreren Schritten verlaufenden
Gesamtreaktion für die Geschwindigkeit der Gesamtreaktion bestimmend
ist.
Die Abhängigkeit der
Reaktionsgeschwindigkeit von der Konzentration der beteiligten Stoffe
beschreibt das Geschwindigkeitsgesetz
einer chemischen Reaktion. Dabei gibt
es - vereinfacht - im Prinzip vier verschiedene
Fälle:
|
|
Fall A: |
Die RG hängt
nicht von der Konzentration irgendeines Ausgangsstoffes ab. |
|
Fall B: |
Die RG hängt
nur von der Konzentration eines Edukts in der 1. Potenz ab, dann
ist die Reaktion 1. Ordnung. |
|
Fall C: |
Die RG hängt
von der Konzentration zweier Ausgangsstoffe in der 1. Potenz oder
eines Ausgangsstoffes in der 2. Potenz ab, dann ist die Reaktion
2. Ordnung. D.h. hier verhält sich die RG proportional zum Quadrat
der Konzentration eines Edukts oder proportional zum Produkt der
Konzentrationen zweier Edukte in einfacher Potenz. |
|
Fall D: |
Die RG ist
3. Ordnung, gebrochener Ordnung oder sogar negativ. |
|
|
Die Gesamtordnung einer Reaktion ist die Summe der Potenzen, zu denen
die einzelnen Konzentrationen im Geschwindigkeitsgesetz erhoben werden.
Die Reaktionsordnung muss
grundsätzlich experimentell bestimmt werden, sie kann nicht aus der
Stöchiometrie der Reaktion (makroskopische Betrachtungsweise)
geschlussfolgert werden. Gleichheiten zwischen Stöchiometrie und
experimentell ermittelter Reaktionsordnung haben keinen ursächlichen
Zusammenhang.
Ausgangslage für die nachfolgende
Betrachtung ist die Reaktion von 2-Brompropan mit Natriumhydroxid
in
methanolischer Lösung:
CH3-CHBr-CH3
+ NaOH –> CH3-CHOH-CH3
+ NaBr
A
+ B
C
+ D
Zu jedem Zeitpunkt der
Reaktion gilt: c(A) = c(OH‾) und c(C) = c(Br‾) .
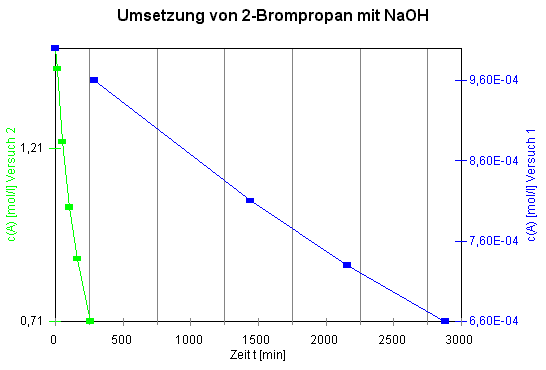
Die Versuchsdaten von Versuch 1 und Versuch 2:1
|
Tabelle 1:
|
Versuch 1 |
Versuch 2 |
|
t [min] |
c(A) = c(OH‾)
[mol/L] |
t [min] |
c(A)=c(OH‾)
[mol/L] |
|
0 |
10*10-4 |
0 |
1,5 |
|
285 |
9,6*10-4 |
11,3 |
1,44 |
|
1440 |
8,1*10-4 |
52,9 |
1,23 |
|
2160 |
7,3*10-4 |
104 |
1,04 |
|
2880 |
6,6*10-4 |
162 |
0,89 |
|
|
|
260 |
0,71 |
 |
|
|
|
Aus den
Konzentrations-Zeit-Diagrammen sind die zugrundeliegenden kinetischen
Zusammenhänge nicht erkennbar,
außer:
Versuch 2 läuft in ca. 10-mal kürzerer
Zeit ab als Versuch 1. Denkbar einfache Zusammenhänge, nämlich lineare, erhält man jedoch, wenn man die
vermuteten differentiellen Zeitgesetze in integrierte Zeitgesetze
umwandelt.
Geschwindigkeitsgesetze - Zeitgesetze
Differentialgleichung des Zeitgesetzes 1. Ordnung:
Im Zeitgesetz 1. Ordnung hängt die
RG nur von der
Konzentration eines Eduktes ab. Trägt man die RG gegen die Konzentration
auf, erhält man eine Gerade, die einer linearen Funktion
entspricht. Die Steigung der Geraden gibt den Wert der Proportionalitätskonstante k an, die somit zur
Geschwindigkeitskonstanten
wird. Die Geschwindigkeitskonstante k
ist eine temperatur- und stoffabhängige Größe und somit unabhängig von
der Konzentration.
vr
= -dc(A)/dt = -k*c(A) = - k*c(OHG) {1}
vr gibt die Konzentrationsänderung von A
in einem verschwindend kleinen Zeitintervall dt an, entspricht also der
Momentangeschwindigkeit. Die
Umwandlung der Differentialgleichung geschieht durch Integration in
mehreren Schritten:
1. Schritt:
Trennung der
Variablen: 1/c(A) * dc(A) = - k*dt {2}
2. Schritt:
Integration in den Grenzen von c=0
(Ausgangskonzentation c0(A) bis c=A und t = 0 bis t = t
c(A)
t
∫1/c(A) * dc(A) = -k *∫dt {3}
c0(A)
0
3. Schritt: Lösung des Integrals: ln c(A) = -k * t +
const. {4}
Ist zu Beginn der Reaktion (t = 0) die Konzentration von A, c(A) = 0,
also c(A) = c0(A), so folgt durch Einsetzen in die letzte Gleichung für die Integrationskonstante: const. = ln c0(A)
{5} .
Somit erhält man:
ln c(A) = ln c0(A) - k*t {6}
oder:
ln c0(A)/c(A)
= k*t {7}
bzw.:
k = 2,303/t * lg (c0(A))/c(A) {8}
oder:
c(A) = c0(A)
* e-k*t
{9}
Die letzte Gleichung beschreibt also die
Abhängigkeit der Konzentration von der Zeit bei einer Reaktion 1.
Ordnung.
Hat man experimentell c(A) als Funktion von t bestimmt, verwendet man
zur Auswertung Gleichung {6} oder {7} und trägt dann ln c(A) bzw. ln c0(A)/c(A) gegen t auf.
Verläuft die Reaktion nach der 1. Ordnung, erhält man eine Gerade mit dem Achsenabschnitt ln c0(A) bzw. eine
Ursprungsgerade, deren Steigung den Wert der Geschwindigkeitskonstanten
k angibt.
|
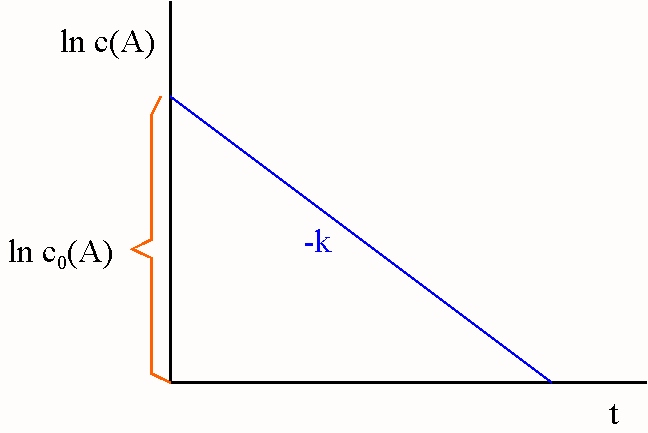
Abb. 2:
Auswertung einer Reaktion 1. Ordnung: Auftragung nach Gleichung
{6} |

Abb. 3:
Auswertung einer Reaktion 1. Ordnung: Auftragung nach Gleichung
{7} |
|
|
Ein
etwas anderer Ansatz
geht von folgenden Ausgangsdefinitionen aus:
Für das Geschwindigkeitsgesetz 1. Ordnung
gilt das differentielle Zeitgesetz in der folgenden Form:
vr
= dx/dt = k*(a-x) {10}
Dabei sind: a = Anfangskonzentration
a-x = die Konzentration des Edukts zum Zeitpunkt t
x = die Konzentration des Edukts, die zum Zeitpunkt t bereits
zerfallen ist.
Die Gleichung dx/dt = k*(a-x) ist eine
Differentialgleichung mit getrennten Variablen. Die Variablen sind x und
t, der Differentialquotient ist dx/dt. Die Lösung der
Differentialgleichung erfolgt durch Trennung der Variablen und
Integration:
1. Trennung der Variablen:
dx / (a-x) = k * dt {11}
2. Integration:
∫ dx / (a-x) = k * ∫ dt {12}
3. Anwendung der Substitutionsmethode:
a-x sei y und -dx sei dy.
Dann gilt: - ∫ dy / y = k * ∫ dt {13}
- ln y = k*t + A {14}
A ist hier die Integrationskonstante oder
die Summe der Integrationskonstanten.
- ln (a-x) = k*t + A {15}
Nun wird die Integrationskonstante durch
die Anfangsbedingungen festgelegt:
Bei t = 0 ist x = 0, somit gilt für -ln (a-x)
= k*t + A dann: -ln a = A {16}.
Damit lautet die
Beziehung zwischen der Konzentration und der
Zeit bei einer Reaktion 1. Ordnung:
- ln (a-x) =
k * t - ln a {17} entspricht der
Gleichung {6}
ln a - ln (a-x) = k * t
{18}
entspricht der Gleichung {7}
oder:
ln a / (a-x) = k * t
{19}
Zur Bestimmung der
Geschwindigkeitskonstanten löst man Gleichung {18} nach k auf und
erhält:
k = 1/t * ln
a / (a-x) {20}
Zur Auswertung ist es nicht nötig, die
wahren Konzentrationen a oder a-y einzusetzen. Es genügt, gemessene
Werte (z.B. Volumenwerte in ml oder Stromstärken in
mA) einzusetzen, da der Quotient a/(a-x) eine dimensionslose Zahl
ist.
|
|
Zusammenfassung:
(Tabelle 2) |
|
|
ln c(A) = ln c0(A)
- k*t {6} |
ln c0(A)/c(A)
= k*t {7} |
c(A) = c0(A)
* e-k*t
{8} |
|
ln (a-x) = ln a - k * t
{17} |
ln a /
(a-x) = k * t {19} |
|
|
|
Wendet man also das Zeitgesetz 1. Ordnung auf
die Daten des Versuchs 1 an, so erhält man die Werte
in Tabelle 3:
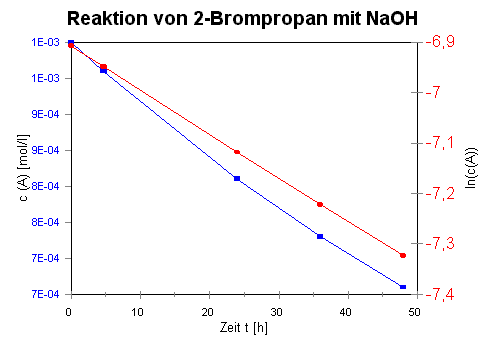
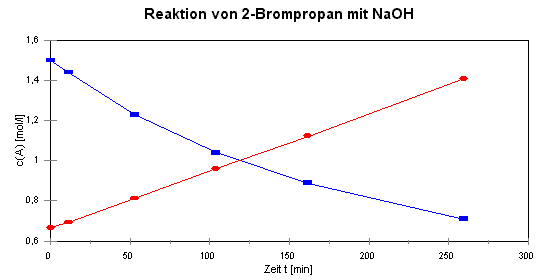
Die graphische Darstellung ergibt das folgende Diagramm: |
Tabelle 3:
|
t [h] |
c(A) [mol/L] |
ln c(A) |
|
0 |
1,00e-03 |
-6,908 |
|
4,75 |
9,60e-04 |
-6,949 |
|
24 |
8,10e-04 |
-7,118 |
|
36 |
7,30e-04 |
-7,222 |
|
48 |
6,60e-04 |
-7,323 |
|
|
Dabei ist die blaue Linie die ursprüngliche Kurve der
Konzentration c(A) gegen t und die rote Linie die
Auftragung der Werte von ln c(A) gegen t. |
|
Die Steigung der Geraden ergibt den
Wert von - k, der Achsenabschnitt entspricht ln c0(A)
.
|
 |
|
|
Das Zeitgesetz in der integrierten Form ist
also:
(A) = c0(A)
* e-k*t
{8}
bzw. c(OHG)
= c0(OHG)*e-k*t
oder:
ln c(A) = ln c0(A)
- k*t {6}
bzw.
ln
c(OHG)
= ln c0(OHG)
- k*t
Besteht eine lineare Abhängigkeit zwischen dem
Logarithmus der Konzentrationswerte und der Zeit, ist damit das
Zeitgesetz 1. Ordnung gegeben.
|
|
Differentialgleichung des Zeitgesetzes 2. Ordnung:
Verläuft die Reaktion zwischen
zwei Stoffen A und B nach einem Zeitgesetz 2. Ordnung, so kann für die
RG gelten:
vr
= -dc(A)/dt = - dc(B)/dt = k*c(A)*c(B) {21}
Das Zeitgesetz kann aber auch
diese Form haben:
vr
= -dc(A)/dt = - dc(B)/dt = k*c(A)2
= k*c(B)2
{22}
Wählt man die
Reaktionsbedingungen so, dass die Anfangskonzentrationen c0(A)
= c0(B)
sind, dann ist die Wahrscheinlichkeit groß, dass auch während des
gesamten Reaktionsverlaufs, zu jedem beliebigen Zeitpunkt c(A) = c(B) = c, wenn Stoff A und Stoff B in
äquivalenten Mengen umgesetzt werden. Es wird also implizit
ausgeschlossen, dass Stoff A oder Stoff B irgendwelche „Umwegreaktionen"
eingehen.
Unter diesen Bedingungen
vereinfacht sich die Gleichung zu {22}: - dc(A)/dt = k*c2
, wobei c = c(A) oder c(B) ist.
Diese Differentialgleichung lässt
sich nach Trennung der Variablen c und t umformen:
1/c2(A)*
dc(A) = - k * dt {23}
Die Integration ergibt den Term
c(A)
t
∫
dc/c2
= - k*
dt ∫
{24}
c0(A)
0
die Lösung des Integrals den Term
-1/c(A) = -k*t + const. {25}
Für die
Integrationskonstante const. ergibt sich der Wert: const = - 1/c0(A)
mit c0
= Anfangskonzentration von Stoff A zum Zeitpunkt t = 0.
Die weitere Umformung von {25} ergibt den
Ausdruck:
1/c(A) = 1/c0(A)
+ k * t {26}
oder
c(A) = c0(A)/
(1 + c0
(A)*k*t) {27}
|
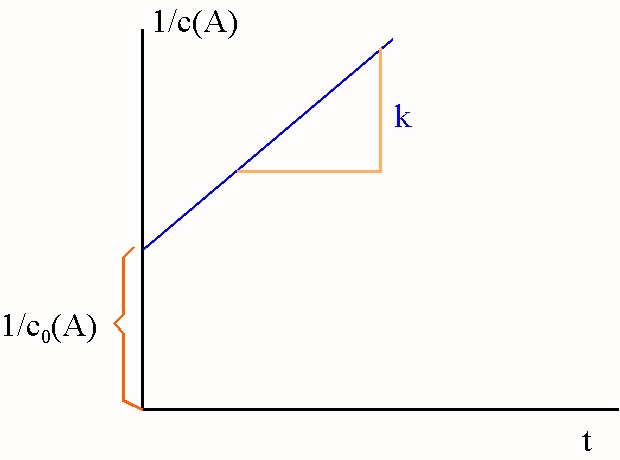 |
Zur Auswertung eines Versuchs,
bei dem c(A) als Funktion
von t bestimmt wurde, trägt man nach Gleichung
{26} 1/c
gegen t auf. Verläuft die Reaktion nach dem
Zeitgesetz 2. Ordnung, erhält man eine Gerade mit dem
Achsenabschnitt
1/c0
, deren Steigung den Wert der Geschwindigkeitskonstanten k angibt. Wendet man also das Zeitgesetz 2.
Ordnung auf die Daten des Versuchs 2 an, so erhält man die
Werte in Tabelle
4: Die graphische Darstellung ergibt das
folgende Diagramm:
|
Tabelle
4:
|
t [min] |
c(A) [mol/L] |
1/c(A) |
|
0 |
1,5 |
0,67 |
|
11,3 |
1,44 |
0,69 |
|
52,9 |
1,23 |
0,81 |
|
104 |
1,04 |
0,96 |
|
162 |
0,89 |
1,12 |
|
260 |
0,71 |
1,41 |
|
 |
|
| Die blaue Linie ist
die ursprüngliche Konzentrations-Zeit-Kurve, die rote Linie ergibt sich
durch Auftragen der
Werte von 1/c gegen die Zeit. Es besteht also
eine lineare Abhängigkeit zwischen dem Kehrwert der Konzentration und der Zeit, was dem Zeitgesetz
der 2. Ordnung entspricht.
|
|
Reaktionsmechanismen |
|
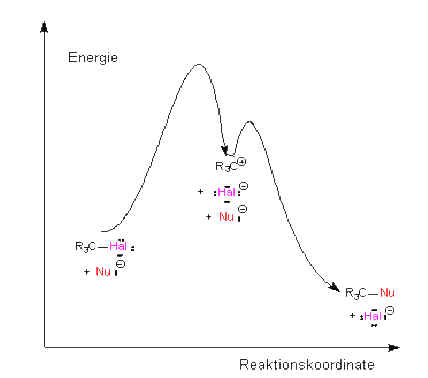
Unimolekulare
Reaktion SN1-Verlauf:
Die nach dem Ge-schwindigkeitsgesetz 1. Ordnung
verlaufende Nucleophile Substitution hängt also nur von der
Konzentration des Sub-strats ab, also von der Konzentration von
2-Brompropan. Die Kon-zentration des Natrium-hydroxids spielt also
offensichtlich keine Rolle. Unter diesen Umständen wird diese
Nucleophile Substitution 1. Ordnung wie folgt erklärt: Im ersten
langsamsten, geschwin-digkeitsbestimmenden Schritt dissoziiert |
 |
| das 2-Brompropan
in ein Bromid-Ion und ein sekundäres Carbenium-Ion, auch Carbokation
genannt. Da dieser Schritt nur von einem Teilchen abhängt, ist es ein sog.
unimolekularer Schritt, die Reaktion also eine unimolekulare Reak-tion.
Dieser geschwin-digkeitsbestimmende Schritt folgt also auf der stofflichen
Ebene der Kinetik 1. Ordnung.
Abb. rechts: Energiediagramm der SN1-Reaktion |
 |
|
Bimolekulare Reaktion - SN2-Verlauf:
Für das Geschwindigkeitsgesetz 2. Ordnung
wird folgender Mechanismus postuliert: In einem ersten
langsamen, geschwindigkeitsbestimmenden Schritt erfolgt die
Bildung eines Tradukts, in dem das C-Atom fünfbindig ist: die
Annäherung des Hydroxid-Ions und die Abspaltung |
 |
|
| des Bromid-Ions erfolgen
gleichzeitig und synchron.
Bindungsbruch und -neubildung finden also
gleichzeitig statt. Für die Bildung des Tradukts braucht es
beide Stoffe: das Substrat und das Agens. Also ist es insgesamt
eine bimolekulare Reaktion, weil für die Ausbildung des
Übergangszustandes beide Stoffe notwendig sind.
Im geschwindigkeitsbestimmenden Schritt
sind beide Konzentrationen in 1. Potenz vorhanden, also folgt
die Kinetik dem Geschwindigkeitsgesetz einer 2. Ordnung.
Die
Reaktionsordnung
muss nicht immer mit der
Molekularität
komplementär dahergehen.
In diesem Fall ist jedoch die Nucleophile Substitution 1. Ordung
eine unimolekulare Reaktion und die Nucleophile Substitution 2.
Ordnung eine bimolekulare Reaktion.
Die Reaktionsordnung muss experimentell
bestimmt werden, spiegelt also einen chemischen Zusammenhang auf
der mathematischen Ebene wider. Die Reaktionsmolekularität ist |
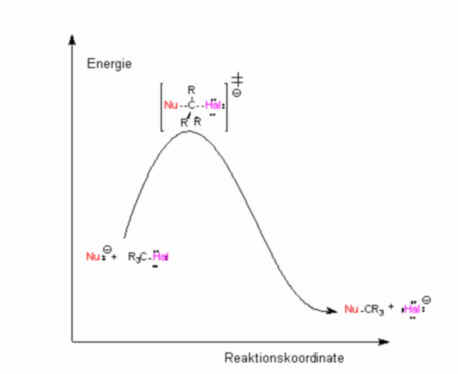
Abb. 7: Energieverlauf der
SN2-Reaktion |
|
| lediglich eine Hypothese
auf der Basis der Reaktionsordnung (u. ggf. andere Fakten und
Untersuchungsmethoden) und bezieht sich auf die Umformung der Teilchen
während der Reaktion, also auf die Teilchenebene. |
|
Wann
verläuft eine Nucleophile Substitution nach dem SN1- oder dem
SN2-Mechanismus?
Bei einer Struktur wie
dem 2-Brompropan hängt dies von der Anfangskonzentration der Edukte ab:
relativ große Anfangskonzentrationen bewirken eine Reaktion nach SN2,
relativ kleine Anfangskonzentrationen eine Reaktion nach SN1. Dazwischen, d.h. bei Konzentrationen
um ca. 0,1 mol/L erhält man beide Reaktionen nebeneinander in Konkurrenz
zueinander.
Ist die Substrat-Struktur
eindeutiger, d.h. kann sie während des Übergangszustandes in der einen
oder anderen Richtung besser stabilisiert werden, läuft
bevorzugt die Nucleophile Substitution nach SN1
oder
SN2 ab.
Wird z.B. durch die
Existenz möglichst vieler Methylgruppen unter dem Einfluss deren
+I-Effekts das dreibindige Carbokation stabilisiert, dann verläuft die
Reaktion bevorzug nach SN1. Gibt es derartige
Stabilisierungsmöglichkeiten für den Übergangszustand nicht, z.B. weil das
Substrat ein primäres C-Atom an der reagierenden Stelle besitzt, wird SN2 bevorzugt.
Das
elektrophile Zentrum
Die Bildung eines Carbeniumions
wird nur dann begünstigt, wenn die positive Ladung durch das Molekül
stabilisiert werden kann. Dies kann bei Alkyl- oder Arylgruppen am
elektrophilen Kohlenstoffatom durch deren +I- oder +M-Effekte geschehen.
Daher wird an einem primären elektrophilen Zentrum eine SN2-Reaktion und
an einem tertiären Zentrum eine SN1-Reaktion begünstigt.
Die Abgangsgruppe
Das Austrittsvermögen der Abgangsgruppe ist mit der Stärke der konjugierten Säure proportional.
Die Spaltung der C-X-Bindung erfolgt umso leichter, je stabiler das
austretende Ion oder je stärker die korrespondierende Säure H-X ist:
I-
> Br-
> Cl-
>> F-
Das
Nukleophil
Die Geschwindigkeit wird mit
zunehmender Nukleophilie des angreifenden Teilchens erhöht:
RS-
> CN-
> I-
> OH-
> Br-
> Cl-
> RCOO-
> H2O
> F-
Das
Lösungsmittel
Lösungsmittel solvatisieren die
Reaktionspartner und den Übergangszustand. Wichtige Eigenschaften sind
ihre Polarität, Solvatationsvermögen und die Fähigkeit,
Wasserstoff-Brückenbindungen
auszubilden. Durch die Auswahl eines Lösungsmittels kann daher das
Verhältnis SN1 zu SN2 gesteuert werden. |
|
Diese Darstellung ist und kann nicht allumfassend die Nucleophile
Substitution behandeln, die einer der am besten untersuchten
Reaktionsmechanismen ist. Bestimmte Aspekte wie die Konfigurationsumkehr
(Inversion, Walden'sche Umkehr), eine genaue Definition von Racemat, die
Wagner-Meerwein-Umlagerung u.a. sind aus Gründen der Übersichtlichkeit
bewusst weggelassen worden. |
|
Literatur:
Flörke/Wolff: Kursthemen Chemie, Allgemeine und Physikalische Chemie
Gerhard Graeb: Reaktionen und Mechanismen, Organische Chemie in der
Kollegstufe, DBV
Heinz Wambach (Hrsg): Materialien-Handbuch Kursunterricht Chemie,
Band 3: Kinetik - Gleichgewichte - Massenwirkungsgesetz, Aulis-Verlag,
Deubner&Co
W. Jansen, B. Ralle, R. Peper: Reaktionskinetik und chemisches
Gleichgewicht, Aulis Kolleg Chemie
P.W. Atkins, J.A. Beran: Chemie - einfach alles, VCH
Tausch / v. Wachtendonk: Chemie SII, Stoff-Formel-Umwelt, C. C.
Buchner
K. H. Näser: Physikalische Chemie; VEB Leipzig 1971
M. Kindler: Organische Chemie Kompakt, CDCH-Verlag Hamburg 2001
Diesen Text
Die
Reaktion von 2-Brompropan mit Natronlauge gibt es auch im
pdf-Format und im
WordPerfect-Format als zip-Dateien.
|
|
|