1. Faraday-Gesetz:
Die elektrolytisch abgeschiedene Stoffmenge n
eines Stoffes X ist der durch den Stromkreis geflossenen Ladung Q
proportional. |
 |
|
2. Faraday-Gesetz:
Die Ladung Q, die zur Abscheidung einer bestimmten
Stoffmenge eines Stoffes X benötigt wird, ist proportional der Anzahl an
Elektronen z, die für die Bildung des Teilchen X |
 |
|
3. Berechnung der
Proportionalitätskonstanten:
Bei der Elektrolyse von Wasser scheiden
sich Wasserstoff- und Sauerstoffgas ab. Die folgende
Tabelle
zeigt den Zusammenhang zum 1. Faraday-Gesetz. |
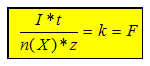 |
| |
U=10 V
I=0,13 A |
U=20 V
I=0,33 A |
| t[min] |
V(H2)[mL] |
V(O2)[mL] |
V(H2)[mL] |
V(O2)[mL] |
| 2 |
1,8 |
0,9 |
4,1 |
2,1 |
| 4 |
3,5 |
1,9 |
8,8 |
4,5 |
| 6 |
5,1 |
2,7 |
13,2 |
6,7 |
| 8 |
6,9 |
3,7 |
17,1 |
8,8 |
| 10 |
8,7 |
4,6 |
21,5 |
11,0 |
| 12 |
10,4 |
5,6 |
25,8 |
13,2 |
| 14 |
12,1 |
6,4 |
30,1 |
15,4 |
| 16 |
14,0 |
7,5 |
34,5 |
17,8 |
| 18 |
15,6 |
8,2 |
38,9 |
19,9 |
| 20 |
17,3 |
9,2 |
43,0 |
22,0 |
|
Allerdings muss das bei einem konkreten Druck
(abweichend vom
Norm[al]druck 1013 hPa
) und einer konkreten Raumtemperatur (abweichend von der
Norm[al]temperatur = 0 °C
oder
Standardtemperatur = 25 °C) gemessene
Volumen erst in ein Normvolumen umgerechnet werden: |
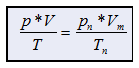
|
p
= realer Druck [hPa]
V
= Gasvolumen des
realen Gases [L, mL]
T
= reale Temperatur
[K]
pn
= Normdruck
1013
hPa
Vm
= molares Gasvolumen [L, mL]
Tn
= Normtemperatur
273 K |
 |
Das molare Gasvolumen bezieht sich auf das
molare Normvolumen
Vmn
= 22414 mL/mol bei 273,15 K und
1013 hPa. |
Mit der Beziehung
|
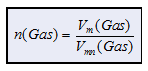 |
wird Vmn in n(Gas) umgerechnet! |
|
|
|
Arbeitsaufträge: |
|
1.
Berechne selbstständig
aus der Tabelle - auf jeden Fall verschieden von deinen/m Nachbarn! -
n(Gas), also
n(H2)
und n(O2)
für ein konkretes, beliebiges Stromstärke-Zeit-Wertepaar. |
|
2.
Berechne daraus für eben
dieses Wertepaar die
Proportionalitätskonstante k = F!
(Faradaykonstante) |
|
3.
Der
wissenschaftliche Wert
der Faraday-Konstante beträgt
96487 C/mol. Diskutiere schriftlich die
Gründe für die Abweichung zwischen wissenschaftlichem und experimentell
bestimmten Wert. |
|
4.
Bestimme die
Elementarladung e
aus dem wissenschaftlichen Wert der
Faraday-Konstante: e = F/NA
mit NA
= 6,023*1023
Teilchen/mol (die Zahlenfolge 23 wird wegen der Eselsbrücke gewählt!) |
5.
Bei der
Elektrolyse von Kupferchlorid CuCl2
entstehen nach 5 Minuten bei einer Stromstärke von 0,1 A an der Anode
3,8 mL Chlorgas bei einer Temperatur von 22 °C und einem Druck von 1000
hPa.
a) Formuliere die Reaktionsgleichungen für
Kathode und Anode!
b) Berechne die geflossene Ladung!
c) Rechne das Chlorvolumen auf Normbedingungen
um!
d) Berechne die elektrolytisch abgeschiedene
Stoffmenge (mol) an Kupfer und Chlor!
e) Berechne die Stoffportion [g] an Kupfer und
Chlor! |
|
|
Lösungen: |
|
Arbeitsaufträge: |
|
1.
Berechne selbstständig aus der Tabelle - auf
jeden Fall verschieden von deinen/m Nachbarn! - n(Gas), also n(H2)
und n(O2) für ein konkretes, beliebiges
Stromstärke-Zeit-Wertepaar. Die
Anleitung, wie man aus den Gasvolumina die Teilchenzahl n(H2)
und n(O2) errechnet, steht in
Zusammenhang Gasvolumen
Ladung.pdf
|
|
2.
Berechne daraus für eben dieses Wertepaar die
Proportionalitätskonstante k = F! (Faradaykonstante)
Nach dem I. Faradayschen Gesetz gilt: "Die
elektrolytisch abgeschiedene
Stoffmenge n eines Stoffes X ist der durch den Stromkreis
geflossenen Ladung Q proportional": n(X)
≈
Q oder n(X) ≈ I * t mit I in [A] und t in [sec]
Nach dem II. Faradayschen Gesetz gilt: "Die Ladung Q,
die zur Abscheidung einer bestimmten Stoffmenge n(X) benötigt wird, ist
proportional der Anzahl an Elektronen z, die für die Bildung des Teilchens X
aufgenommen oder abgegeben werden": Q
≈ n(X) * z
Damit ergibt sich aus der Division von Q / n(X) * z
eine Proportionalitätskonstante, die Faraday-Konstante:
Q / n(X) * z = k = F
|
Ermittlung der
Faraday-Konstanten für die 1. und 2. Versuchsreihe |
| Divisionsfaktor |
2 |
4 |
2 |
4 |
|
|
V1(H2) |
V1(O2) |
V2(H2) |
V2(O2) |
|
| |
107.213 |
100.442 |
118.156 |
115.342 |
|
| |
107.515 |
100.442 |
110.100 |
107.653 |
|
| |
112.258 |
106.022 |
110.100 |
108.456 |
|
| |
110.631 |
103.156 |
113.319 |
110.100 |
|
| |
109.678 |
103.717 |
112.660 |
110.100 |
|
| |
110.100 |
102.235 |
112.660 |
110.100 |
|
| |
110.403 |
104.365 |
112.660 |
110.100 |
|
| |
109.051 |
101.781 |
112.333 |
108.862 |
|
| |
110.454 |
104.729 |
112.081 |
109.546 |
|
| |
110.312 |
103.717 |
112.660 |
110.100 |
|
| |
109.761 |
103.061 |
112.673 |
110.036 |
|
| Mittelwert |
109.761 |
103.061 |
112.673 |
110.036 |
|
| Abweichung |
13,76% |
6,82% |
16,78% |
14,04% |
12,85% |
| |
V = 10 V |
V = 20 V |
|
|
|
|
3.
Der wissenschaftliche Wert der Faraday-Konstante beträgt 96487 C/mol.
Diskutiere schriftlich die Gründe für die Abweichung zwischen
wissenschaftlichem und experimentell bestimmten Wert.
Die Abweichung vom wissenschaftlichen Wert ergibt sich weitgehend aus
experimentellen Ungenauigkeiten, die mit der Messung von Gasvolumina
verknüpft sind: Luftdruck und Lufttemperatur werden nur ungefähr genau
bestimmt, das elektrolysierte Wasser muss sich erst mit den Gasen
sättigen, die Ablesegenauigkeit von Volumina ist bei den benutzen
Geräten gering. Die Messung der Stromstärke ist ebenfalls nicht
besonders genau.
|
|
4.
Bestimme die Elementarladung e aus dem wissenschaftlichen Wert der
Faraday-Konstante: e = F/NA mit NA
= 6,023*1023 Teilchen/mol (die Zahlenfolge 23 wird wegen der
Eselsbrücke gewählt!)
e = F / NA = 96487 C/mol / 60,23 * 1023
=
1,60 * 10-19 C
|
|
5.
Bei der Elektrolyse von Kupferchlorid CuCl2 entstehen nach 5
Minuten bei einer Stromstärke von 0,1 A an der Anode 3,8 mL Chlorgas bei
einer Temperatur von 22 °C und einem Druck von 1000 hPa.
a) Formuliere die
Reaktionsgleichungen
für Kathode und Anode!
Kathodenreaktion
= Minus-Pol: Cu2+(aq) + 2 e ̶
----> Cu(s)
Anodenreaktion
= Plus-Pol: 2 Cl
̶ (aq) ----> Cl2(g) + 2 e ̶
b) Berechne die
geflossene Ladung!
Q = 0,1 A * 300 s = 30 As = 30 C
c) Rechne das Chlorvolumen
auf Normbedingungen um!
Unter Normbedingungen
ergibt sich für das Chlorvolumen: p * V(X) / T = pn + Vmn(Cl2)
/ Tn
Vmn(Cl2)
= p * V(Cl2) * Tn / pn * T = 1000
hPa * 3,8 mL * 273 K / 1013 hPa * 295 K =
3,5 mL
d) Berechne die
elektrolytisch abgeschiedene
Stoffmenge (mol) an Kupfer und Chlor!
Damit ergibt sich die Stoffmenge an Chlor:
n(Cl2) = Vmn(Cl2) / Vmn = 3,5 * 10-3
L / 22,4 l*mol-1 = 0,00016 mol
e) Berechne die
Stoffportion [g] an Kupfer und Chlor!
Aus der Reaktionsgleichung wird deutlich, dass
für ein Mol Chlor-Moleküle ein Mol Kupfer-Atome abgeschieden werden. Die damit
abgeschiedene Stoffmenge an Kupfer n(Cu) = 0,00016 mol.
Stoffportion m(Cl2)
=
0,01136 g
Stoffportion m((Cu) =
0,01 g
Siehe dazu
auch
Elektrolyse und Faraday-Gesetz
im pdf-Format und
Elektrolyse und Faraday-Gesetz im WordPerfect-Format |
update:
02.02.2021
zurück
zur Hauptseite |
|